Statistics is a
mathematical science pertaining to the collection, analysis, interpretation or
explanation and presentation of data. It provides tools for predicting and
forecasting the economic, marketing, and other activities.
Meaning of Statistics: Statistics is concerned with scientific methods for
collecting, organizing, summarizing, presenting, and analyzing data as well as
deriving valid conclusions and making reasonable decisions on the basis of this
analysis. Statistics is concerned with the systematic collection of numerical
data and its interpretation. The word ‘statistic’ is used to refer to 1.
Numerical facts, such as the number of people living in particular area. 2. The
study of ways of collecting, analyzing and interpreting the facts.
TYPES OF STATISTICS:
1. Descriptive Statistics consists of methods for organizing, displaying, and
describing data by using tables, graphs, and summary measures.
2. Inferential Statistics consists of methods that use sample results to help make decisions
or predictions about a population.
DESCRIPTIVE STATISTICS
Descriptive statistics is the term given to the analysis of
data that helps describe, show or summarize data in a meaningful way such that,
for example, patterns might emerge from the data. Descriptive statistics do
not, however, allow us to make conclusions beyond the data we have analyzed or
reach conclusions regarding any hypotheses we might have made. They are simply
a way to describe our data.
Descriptive statistics are very important because if we
simply presented our raw data it would be hard to visualize what the data was
showing, especially if there was a lot of it. Descriptive statistics therefore
enables us to present the data in a more meaningful way, which allows simpler
interpretation of the data. For example, if we had the results of 100
pieces of students' coursework, we may be interested in the overall performance
of those students. We would also be interested in the distribution or spread of
the marks. Descriptive statistics allow us to do this.
Typically, there are five general types of statistics that
are used to describe data:
A. Frequency table In
statistics, a frequency distribution is a list, table or graph that displays
the frequency of various outcomes in a sample. Each entry in the table contains
the frequency or count of the occurrences of values within a particular group
or interval. B. Measures of central tendency (Mean, Median &
Mode)Measures of central tendency: these
are ways of describing the central position of a frequency distribution for a
group of data. In this case, the frequency distribution is simply the
distribution and pattern of marks scored by the 100 students from the lowest to
the highest. We can describe this central position using a number of statistics,
including mode, median and mean. Read more about Measures of Central Tendency by clicking the
link Measures of central tendency
C. Measures of spread or Dispersion: Variance, Range Measures of spread or Dispersion: these are ways of summarizing a group of data by describing
how spread out the scores is. For example, the mean score of our 100 students
may be 65 out of 100. However, not all students will have scored 65 marks.
Rather, their scores will be spread out. Some will be lower and others higher.
Measures of spread help us to summarize how spread out these scores are. To
describe this spread, a number of statistics are available to us, including the
range, quartiles, absolute deviation, variance and standard deviation.
When we use descriptive statistics
it is useful to summarize our group of data using a combination of tabulated
description (i.e., tables), graphical description (i.e., graphs and charts) and
statistical commentary (i.e., a discussion of the results).
Measures of spread describe how similar or varied the set of observed values
are for a particular variable (data item). Measures of spread include:1. Range 2. variance 3. Standard Deviation Read more about Range, Variance and Standard Deviation by clicking the links: Range Mean Deviation Standard Deviation D. Distribution - Skewness and Kurtosis The distribution is a mathematical function that describes the
relationship of observations of different heights. A distribution is simply
a collection of data, or scores, on a variable. Usually, these scores are
arranged in order from smallest to largest and then they can be presented
graphically.
a. Skewness - Skewness is a measure
of symmetry, or more precisely, the lack of symmetry. A distribution, or data
set, is symmetric if it looks the same to the left and right of the center
point. Skewness characterizes the degree of asymmetry of a distribution around
its mean.
The
concept of skewness is mainly used to understand the distribution of the
data and steps taken to normalize the data for further building of machine learning models. In
case of negatively skewed data, Mean<Median<Mode. This indicates, more
data points are to the right of the curve here the data has very high values in
large numbers.
b. Kurtosis - Kurtosis
characterizes the symmetric distribution through the relative peaks or flatness
of the curve. Kurtosis is a measure of whether the data are heavy-tailed or
light-tailed relative to a normal distribution.
The
main difference between Skewness and Kurtosis is: Skewness
measures the degree of the slope in the frequency distribution. Kurtosis
measures the degree of thickness in the tails of the distribution curve.
There are 3 types of Kurtosis: • Platykurtic (relatively flat) • Mesokurtic (normal) • Leptokurtic (relatively peaked)
E. Measures of Position ( Percentile, Quartile ) What is Percentile? Percentiles
indicate the percentage of scores that fall below a particular value. They tell
you where a score stands relative to other scores. For example, a person with
an IQ of 120 is at the 91st percentile, which indicates that their IQ is higher
than 91 percent of other scores.
Percentiles are a great tool to use when you need to know the relative
standing of a value. Where does a value fall within a distribution of values?
While the concept behind percentiles is straight forward, there are different mathematical
methods for calculating them. In this post, learn about percentiles, special
percentiles and their surprisingly flexible uses, and the various procedures
for calculating them.
Using
Percentiles to Understand a Score or Value - Percentiles
tell you how a value compares to other values. The general rule is that if
value X is at the kth percentile, then X is greater than K% of the values. What
Is a Quartile? A quartile is a statistical term that describes a
division of observations into four defined intervals based on the values of the
data and how they compare to the entire set of observations.
Understanding
Quartiles To understand the quartile, it is important to understand the median as
a measure of central tendency. The median in statistics is the middle value of
a set of numbers. It is the point at which exactly half of the data lies below
and above the central value. So, given a set of 13 numbers, the median would be
the seventh number. The six numbers preceding this value are the lowest numbers
in the data, and the six numbers after the median are the highest numbers in
the dataset given. Because the median is not affected by extreme values or
outliers in the distribution, it is sometimes preferred to the mean. The median
is a robust estimator of location but says nothing about how the data on either
side of its value is spread or dispersed. That's where the quartile steps in.
The quartile measures the spread of values above and below the mean by dividing
the distribution into four groups. How
Quartiles Work Just like the median divides the data into half so
that 50% of the measurement lies below the median and 50% lies above it, the
quartile breaks down the data into quarters so that 25% of the measurements are
less than the lower quartile, 50% are less than the median, and 75% are less
than the upper quartile.
A quartile
divides data into three points—a lower quartile, median, and upper quartile—to
form four groups of the dataset. The lower quartile, or first quartile, is
denoted as Q1 and is the middle number that falls between the smallest value of
the dataset and the median. The second quartile, Q2, is also the median. The
upper or third quartile, denoted as Q3, is the central point that lies between
the median and the highest number distribution.
Now,
we can map out the four groups formed from the quartiles. The first group of
values contains the smallest number up to Q1; the second group includes Q1 to
the median; the third set is the median to Q3; the fourth category comprises Q3
to the highest data point of the entire set. Each quartile contains 25% of the total observations. Generally,
the data is arranged from smallest to largest: 1. First quartile: the lowest 25% of numbers 2. Second quartile: between 25.1% and 50% (up to the
median) 3. Third quartile: 50.1% to 75% (above the median) 4. Fourth
quartile: the highest 25% of numbers
INFERENTIAL STATISTICS Inferential statistics are the statistical procedures
that are used to reach conclusions about associations between variables. They
differ from descriptive statistics in that they are explicitly designed
to test hypotheses.
Inferential statistics is mainly used to derive estimates about a
large group (or population) and draw conclusions on the data based on
hypotheses testing methods. Inferential statistics makes use of sample data because it is more
cost-effective and less tedious than collecting data from an entire population.
It allows one to come to reasonable assumptions about the larger population
based on a sample’s characteristics. Sampling methods need to be unbiased and
random for statistical conclusions and inferences to be validated. Inferential statistics is strongly associated with the logic of
hypothesis testing.
With inferential statistics, you are trying to reach conclusions
that extend beyond the immediate data alone. For instance, we use inferential
statistics to try to infer from the sample data what the population might
think.
Or, we use inferential statistics to make judgments of the probability
that an observed difference between groups is a dependable one or one that
might have happened by chance in this study. Thus, we use inferential
statistics to make inferences from our data to more general conditions; we use
descriptive statistics simply to describe what’s going on in our data. Inferential statistics are useful in experimental and
quasi-experimental research design or in program outcome evaluation.
Perhaps one
of the simplest inferential test is used when you want to compare the average
performance of two groups on a single measure to see if there is a difference.
You might want to know whether eighth-grade boys and girls differ in math test
scores or whether a program group differs on the outcome measure from a control
group. Whenever you wish to compare the average performance between two groups
you should consider the t-test for differences between groups. Most of the major inferential statistics come from a general family of statistical models known as the General Linear Model. This includes the t-test, Analysis of Variance (ANOVA), Analysis of Covariance (ANCOVA), regression analysis, and many of the multivariate methods like factor analysis, multidimensional scaling, cluster analysis, discriminant function analysis, and so on. Given the importance of the General Linear Model, it’s a good idea for any serious social researcher to become familiar with its workings. The discussion of the General Linear Model here is very elementary and only considers the simplest straight-line model. However, it will get you familiar with the idea of the linear model and help prepare you for the more complex analyses described below.
Thus, Inferential statistics helps to suggest explanations for a situation or phenomenon. It allows you to draw conclusions based on extrapolations and is in that way fundamentally different from descriptive statistics that merely summarize the data that has actually been measured.
The most common methodologies in inferential statistics are hypothesis tests, confidence intervals, and regression analysis. Interestingly, these inferential methods can produce similar summary values as descriptive statistics, such as the mean and standard deviation. The following types of inferential statistics are extensively used and relatively easy to interpret:
1. Pearson Correlation
2. Regression
3. T-test
4. Factor Analysis
5. Disciminant analysis
CORRELATION AND LINEAR REGRESSION The most commonly used techniques for investigating the relationship between two quantitative variables are correlation and linear regression.
• Correlation quantifies the strength of the linear relationship between a pair of variables
• Correlation is a single statistic, or data point
• Correlation shows the relationship between the two variables
• Regression expresses the relationship in the form of an equation.
• Regression is the entire equation with all of the data points that are represented with a line.
• Regression allows us to see how one affects the other
It all comes down to correlation and regression, which are statistical analysis measurements used to find connections between two variables, measure the connections, and make predictions. Measuring correlation and regression is commonly used in a variety of industries, and it can also be seen in our daily lives.
For instance, have you ever seen someone driving an expensive car and automatically thought that the driver must be financially successful? Or how about thinking that the further you run on your morning workout, the more weight you’ll lose?
Both of these are examples of real-life correlation and regression, as you’re seeing one variable (a fancy car or a long workout) and then seeing if there is any direct relation to another variable (being wealthy or losing weight). As we investigate the relationships between two variables, it’s important to know the differences and the similarities between correlation and regression.
Correlation vs. regression - Its not uncommon for correlation and regression to be confused for one another as correlation can often drive into regression. However, there is a key difference.
What is the difference between correlation and regression?
The difference between these two statistical measurements is that correlation measures the degree of a relationship between two variables (x and y), whereas regression is how one variable affects another.
Basically, you need to know when to use correlation vs. regression. Use correlation for a quick and simple summary of the direction and strength of the relationship between two or more numeric variables. Use regression when you’re looking to predict, optimize, or explain a number response between the variables (how x influences y).
What is correlation? When
it comes to correlation, think of it as the combination of the words “co”
meaning together and “relation” meaning a connection between two quantities. In
this sense, correlation is when a change to one variable is then followed by a
change in another variable, whether it is direct or indirect. Variables are
considered “uncorrelated” when a change in one does not affect the other. In
short, it measures the relationship between two variables. For
example, let’s say our two variables are x and y. The changes
between these two variables can be considered positive or negative. A positive
change would be when two variables move in the same direction, meaning an
increase in one variable result in an increase in another variable. So, if an
increase in x increases y, it’s positively correlated. An
example of this would be demand and price. This is because an increase in
demand causes the corresponding increase in price. The price would increase
because there are more consumers who want it are willing to pay more for it. If
two variables are moving in opposite directions, like when an increase in one
variable results in a decrease in another, this is known as a negative
correlation. An example of a negative correlation would be the price and demand
for a product because an increase in price (x) results in a decrease in
demand (y). Knowing
how two variables are correlated allows for predicting trends in the future, as
you’ll be able to understand the relationship between the variables — or if
there's no relationship at all.
Correlation analysis The main purpose of correlation, through the lens of correlation analysis, is to allow experimenters to know the association or the absence of a relationship between two variables. When these variables are correlated, you’ll be able to measure the strength of their association. Overall, the objective of correlation analysis is to find the numerical value that shows the relationship between the two variables and how they move together. One key benefit of correlation is that it is a more concise and clear summary of the relationship between the two variables than you’ll find with regression.
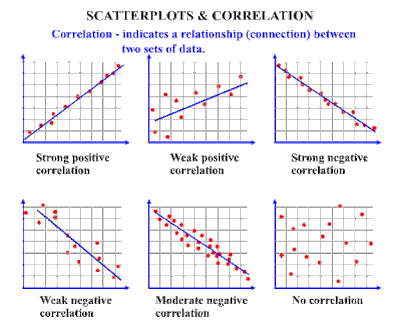
Example of correlation A correlation chart, also known as a scatter diagram, makes it
easier to visually see the correlation between two variables. Data in a
correlation chart is represented by a single point. In the chart above you can
see that correlation plots various points of single data. Let's think of
correlation as real-life scenarios. In addition to the price and demand
example, let's take a look at correlation from a marketing standpoint to see
the strength of a relationship between the two variables. For instance, it
could be in your company's best interest to see if there is a predictable
relationship between the sale of a product and factors like weather,
advertising, and consumer income.
What is regression? On the other hand, regression is how one variable affects another,
or changes in a variable that trigger changes in another, essentially cause and
effect. It implies that the outcome is dependent on one or more variables. For instance, while correlation can be defined as the relationship between two variables, regression is how they affect each other. An example of this would be how an increase in rainfall would then cause various crops to grow, just like a drought would cause crops to wither or not grow at all.
Regression analysis Regression analysis helps to determine the functional relationship between two variables (x and y) so that you’re able to estimate the unknown variable to make future projections on events and goals.
The main objective of regression analysis is to estimate the values of a random variable (z) based on the values of your known (or fixed) variables (x and y). Linear regression analysis is considered to be the best fitting line through the data points. Let’s use the example of tracking the value of a single share in the stock market over the years. X will be time in years and Y will be the value in dollars. We know that the value of a stock is changed by time passing, among other things. We can’t control those other things, but we can control when we sell the stock, so we control the time variable. But how dependent is the value of a stock on time passed? If we bought a stock for $1 and in one year its value went up to $100, does that mean every year the value will go up another $100? Does that mean in 25 years it will be valued at $2500? We don’t know. We figure it out by looking at how much the stock earned over several years. That’s fairly simple because we’re only measuring how much we change one thing or one variable. Then we put those measurements on a graph or plot. The dots could be all over the place or scattered. Could we draw a line through the dots that would show a trend? Let’s call that a trendline. Yes, we can certainly try. That line is a simple linear regression trendline through a scatter plot. For e.g. given below if the data of increase in share price year after year for 20 years. Time (Yrs) and stock value: 2000 - 1498, 2001 - 1160, 2002 - 1147, 2003 - 848.
The main advantage in using regression within your analysis is
that it provides you with a detailed look of your data (more detailed than
correlation alone) and includes an equation that can be used for predicting and
optimizing your data in the future. When the line is drawn using regression, we can see two pieces of
information: Regression
formula A → refers to the y-intercept, the value of y when x = 0 B
→ refers to the slope, or rise over run The prediction formula used to see how data could look in the
future is: Y = a + b(x)
Differences between correlation and regression
There are some key differences between correlation and regression
that are important in understanding the two.
• Regression
establishes how x causes y to change, and the results will change
if x and y are swapped. With correlation, x and y are
variables that can be interchanged and get the same result.
• Correlation is a single statistic, or data point, whereas
regression is the entire equation with all of the data points that are
represented with a line. • Correlation shows the relationship between the two variables,
while regression allows us to see how one affects the other.
• The data shown with regression establishes a cause and effect,
when one changes, so does the other, and not always in the same direction. With
correlation, the variables move together.
Similarities between correlation and regression
In addition to differences, there are some key similarities
between correlation and regression that can help you to better understand your
data. • Both work to quantify the direction and strength of the
relationship between two numeric variables.
• Any time the correlation is negative, the regression slope (line
within the graph) will also be negative.
• Any time the correlation is positive, the regression slope (line
within the graph) will be positive. So much more than just cause and effect
•
Even though they’re studied together, it’s clear that there are
obvious differences and similarities between correlation and regression. When
you’re looking to build a model, an equation, or predict a key response, use
regression. If you’re looking to quickly summarize the direction and strength
of a relationship, correlation is your best bet.
T-Test
A t-test is a type of inferential statistic used to determine if
there is a significant difference between the means of two groups, which may be
related in certain features. It is mostly used when the data sets, like the
data set recorded as the outcome from flipping a coin 100 times, would follow a
normal distribution and may have unknown variances. A t-test is used as a
hypothesis testing tool, which allows testing of an assumption applicable to a
population.
For example:
•
• Compare if the people of one country are taller than people of
another one.
•
• Compare if the brain of a person is more activated while
watching happy movies than sad movies.
This comparison can be analyzed by conducting different
statistical analysis, such as t-test
Factor analysis:
Factor analysis is a way to condense the data in many variables
into a just a few variables. For this reason, it is also sometimes called
“dimension reduction.” You can reduce the “dimensions” of your data into one or
more “super-variables.” The most common technique is known as Principal
Component Analysis (PCA). Factor analysis is used to uncover the latent
structure of a set of variables. It reduces attribute space from a large
no. of variables to a smaller no. of factors and as such is a non dependent
procedure.
Example.
What
underlying attitudes lead people to respond to the questions on a political
survey as they do? Examining the correlations among the survey items reveals
that there is significant overlap among various subgroups of items--questions
about taxes tend to correlate with each other, questions about military issues
correlate with each other, and so on. With factor analysis, you can investigate
the number of underlying factors and, in many cases, identify what the factors
represent conceptually. Additionally, you can compute factor scores for each
respondent, which can then be used in subsequent analyses. For example, you
might build a logistic regression model to predict voting behavior based on
factor scores.
Discriminant analysis
Discriminant analysis is a versatile statistical method often
used by market researchers to classify observations into two or more groups or
categories. In other words, discriminant analysis is used to assign objects
to one group among a number of known groups. By performing discriminant
analysis, researchers are able to address classification problems in which two
or more groups, clusters, or populations are known up front, and one or more
new observations are placed into one of the known classifications based on
measured characteristics.
Discriminant analysis is also used to investigate how variables
contribute to group separation, and to what degree. For this reason, it’s often
leveraged to compliment the findings of cluster analysis.
Market researchers are continuously faced with situations in which
their goal is to obtain a better understanding of how groups (customers, age
cohorts, etc.) or items (brands, ideas, etc.), differ in terms of a set of
explanatory or independent variables.
These situations are where discriminant analysis serves as a
powerful research and analysis tool.
Ref: Dr. Hanif Lakdawala's AMR Notes
